弗洛伊德算法介绍

• 和迪杰斯特拉算法一 样， 弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。
• 弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径
• 迪杰斯特拉算法用于计算图中某-一个顶点到其他项点的最短路径。
• 弗洛伊德算法VS迪杰斯特拉算法:迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他项点的最短路径:弗洛伊德算法中每-个顶点都是出发访问点，所以需要将每-一个顶点看做被访问顶点，求出从每一个顶点到其他顶点的最短路径。
• 算法的时间复杂度为O(N3)，空间复杂度为O(N2)。
• 优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。
• 缺点：时间复杂度比较高，不适合计算大量数据。

弗洛伊德算法思想

通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；

最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵

同时还可引入一个后继节点矩阵path来记录两点间的最短路径。

采用的是(松弛技术)，对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);

其状态转移方程如下： map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}

map[i,j]表示i到j的最短距离，K是穷举i,j的断点，map[n,n]初值应该为0.当然，如果这条路没有通的话，还必须特殊处理，比如没有map[i,k]这条路

算法原理

Floyd算法的原理是动态规划。

设Di,j,k为从i到j的只以(1…k)集合中的节点为中间节点的最短路径的长度。

代码实现：

public class Test1 {
    public static void main(String[] args) {
        System.out.println("请输入有几个顶点：");
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        char[] vertex = new char[n];
        System.out.println("请输入各个顶点的符号，每个字符用空格分隔：");
        for (int i = 0; i  " + vertex[j] + " 的最短路径 " + dis[i][j] + " )    ");
            }
            System.out.println();
        }
    }
    // 弗洛伊德算法
    public void floyd() {
        int len = 0;
        // 从中间节点进行遍历
        for (int k = 0; k 

结果展示：

示例1：

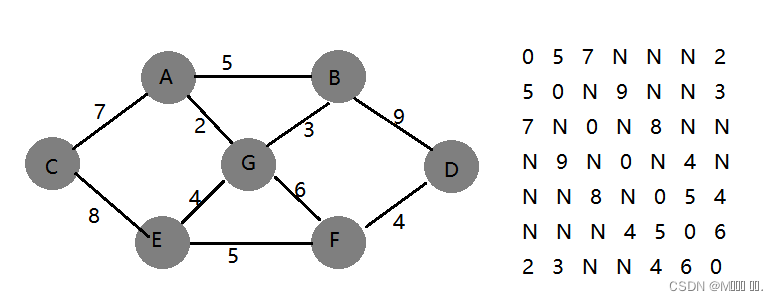
结果：

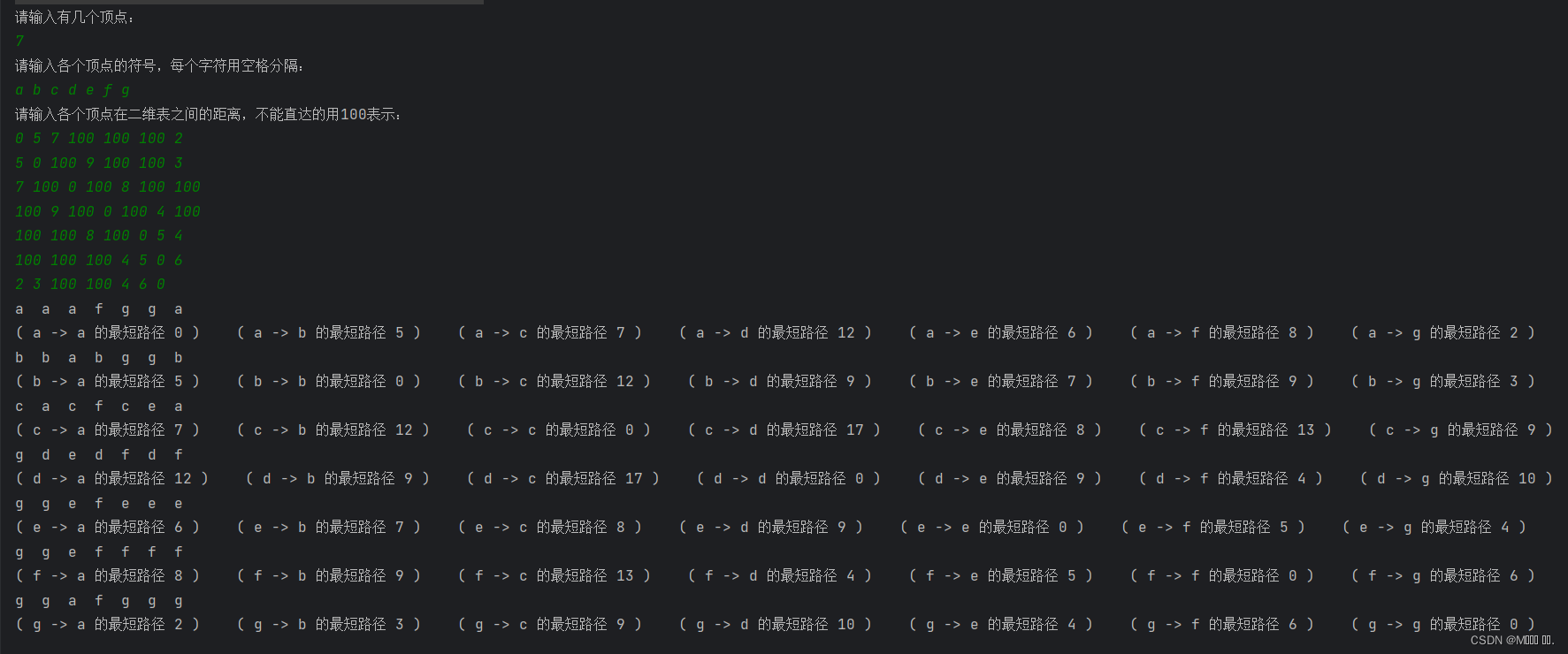
 示例2：

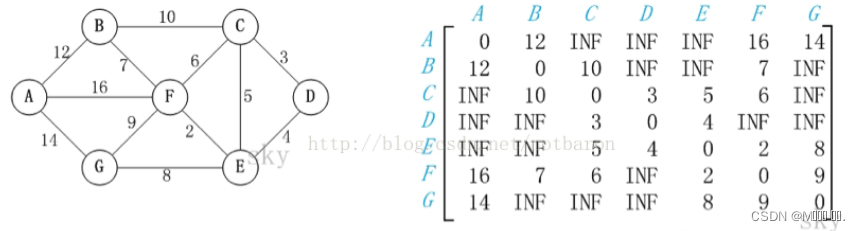
 结果：

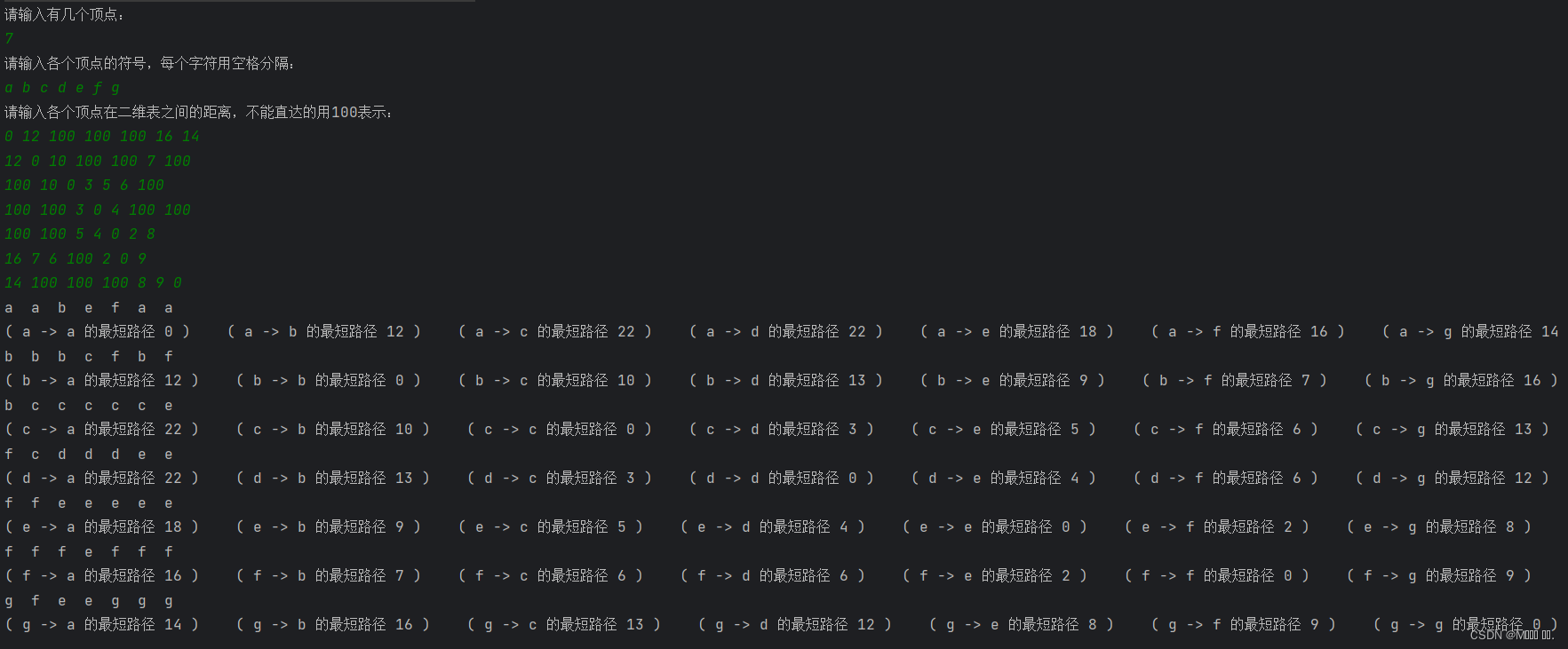
到此这篇关于关于弗洛伊德算法求最短路径详解的文章就介绍到这了,更多相关弗洛伊德算法内容请搜索IT俱乐部以前的文章或继续浏览下面的相关文章希望大家以后多多支持IT俱乐部！