前情提要
如果想优雅地绘制一个足球,那首先需要绘制正二十面体:用Python绘制正二十面体
其核心代码为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | import numpy as npfrom itertools import productG = (np.sqrt(5)-1)/2def getVertex(): pt2 = [(a,b) for a,b in product([1,-1], [G, -G])] pts = [(a,b,0) for a,b in pt2] pts += [(0,a,b) for a,b in pt2] pts += [(b,0,a) for a,b in pt2] return np.array(pts)def getDisMat(pts): N = len(pts) dMat = np.ones([N,N])*np.inf for i in range(N): for j in range(i): dMat[i,j] = np.linalg.norm([pts[i]-pts[j]]) return dMatpts = getVertex()dMat = getDisMat(pts)# 由于存在舍入误差,所以得到的边的数值可能不唯一ix, jx = np.where((dMat-np.min(dMat)) |
为了克服plot_trisurf在xy坐标系中的bug,需要对足球做一点旋转,所以下面要写入旋转矩阵。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | # 将角度转弧度后再求余弦cos = lambda th : np.cos(np.deg2rad(th))sin = lambda th : np.sin(np.deg2rad(th))# 即 Rx(th) => MatrixRx = lambda th : np.array([ [1, 0, 0], [0, cos(th), -sin(th)], [0, sin(th), cos(th)]])Ry = lambda th : np.array([ [cos(th), 0, sin(th)], [0 , 1, 0], [-sin(th), 0, cos(th)]])Rz = lambda th : np.array([ [cos(th) , sin(th), 0], [-sin(th), cos(th), 0], [0 , 0, 1]]) |
最后得到的正二十面体为
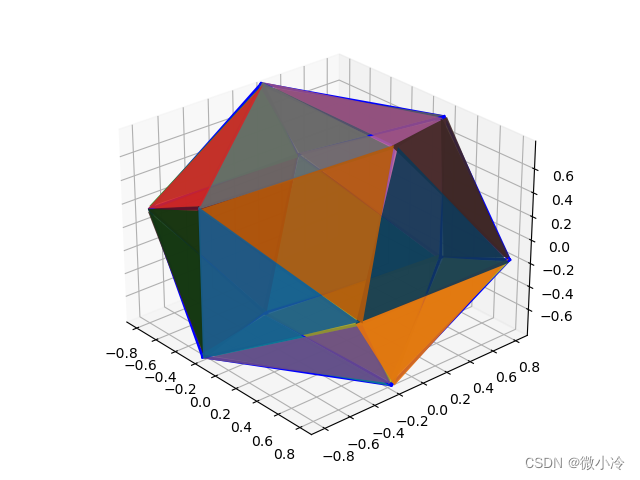
先画六边形
足球其实就是正二十面体削掉顶点,正二十面体有20个面和12个顶点,每个面都是三角形。削掉顶点对于三角形而言就是削掉三个角,如果恰好选择在1/3的位置削角,则三角形就变成正六边形;而每个顶点处刚好有5条棱,顶点削去之后就变成了正五边形。
而正好足球的六边形和五边形有着不同的颜色,所以可以分步绘制,先来搞定六边形。
由于此前已经得到了正二十面体的所有面,同时还有这个面对应的所有边,故而只需在每一条边的1/3 和2/3处截断,就可以得到足球的正六边形。
1 2 3 4 5 6 7 8 9 10 11 12 | def getHexEdges(face): pts = [] for st,ed in face: pts.append((2*st+ed)/3) pts.append((st+2*ed)/3) return np.vstack(pts)ax = plt.subplot(projection='3d')for f in faces: pt = getHexEdges(f) pt = Rx(1)@Ry(1)@pt.T ax.plot_trisurf(*pt, color="white") |
于是,一个有窟窿的足球就很轻松地被画出来了
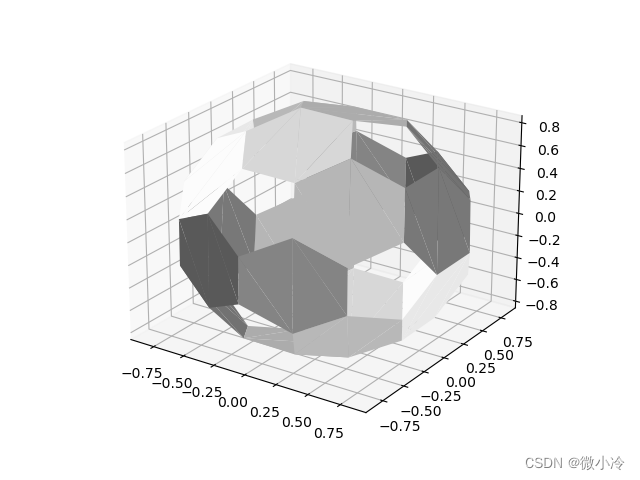
再画五边形
接下来要做的是,将五边形的窟窿补上,正如一开始说的,这个五边形可以理解为削去顶点而得到的,所以第一件事,就是要找到一个顶点周围的所有边。具体方法就是,对每一个顶点遍历所有边,如果某条边中存在这个顶点,那么就把这个边纳入到这个顶点的连接边。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | def getPtEdges(pts, edges): N = len(pts) pEdge = [[] for pt in pts] for i,e in product(range(N),edges): if (pts[i] == e[0]).all(): pt = (2*pts[i]+e[1])/3 elif (pts[i] == e[1]).all(): pt = (2*pts[i]+e[0])/3 else: continue pEdge[i].append(pt) return np.array(pEdge)pEdge = getPtEdges(pts, edges) |
接下来,就可以绘制足球了
1 2 3 4 5 6 7 8 9 10 11 | ax = plt.subplot(projection='3d')for f in faces: pt = getHexEdges(f) pt = Rx(1)@Ry(1)@pt.T ax.plot_trisurf(*pt, color="white")for pt in pEdge: pt = Rx(1)@Ry(1)@pt.T ax.plot_trisurf(*pt, color="black")plt.show() |
效果为
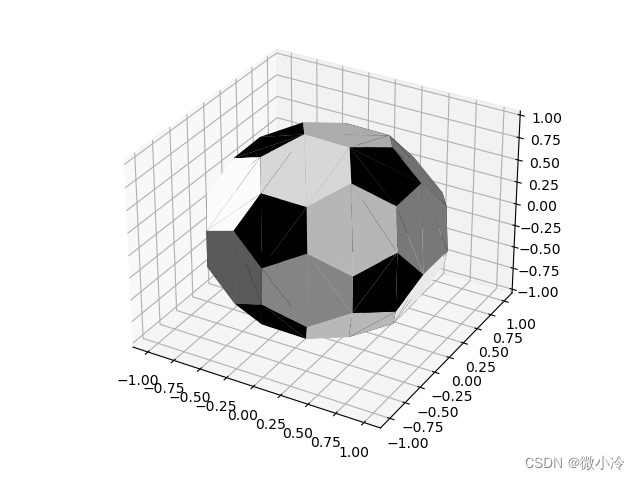
以上就是基于Python实现绘制一个足球的详细内容,更多关于Python足球的资料请关注IT俱乐部其它相关文章!

